Geog 258: Maps and GIS

January 25, 2006

Earth Coordinate

Reading: Chapter 1 (The Earth and Earth Coordinates)

Outlines

Understand different ways to pinpoint the location of a feature shown on a map. Seattle is said to be located at 47.588855 degree latitude North and 122.31665 degree longitude West. How is this value determined? Defining the location of a feature precisely requires placing the location value in a coherent reference system. It begins with thinking of the earth as some kind of model. Here we will talk about three different models of earth (1) earth as a sphere (2) earth as an oblate ellipsoid (3) earth as a geoid. After we understand how the earth is seen as different models, we can define different ways of pinpointing the location.

· Earth as a sphere → horizontal datum (geographic coordinates)

· Earth as an oblate ellipsoid → horizontal datum (geodetic coordinates)

· Earth as a geoid → vertical datum

How did Eratosthenes measure earth’s circumference?

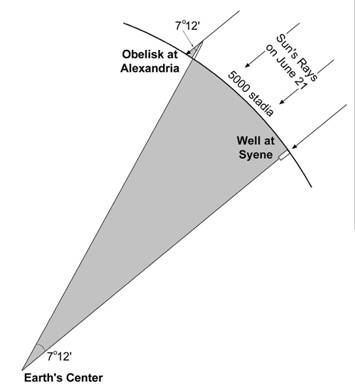
Angle of shadow at Alexandria is 7 degree 12 minute

Angle of shadow at Syene is 90 degree

Distance between Alexandria and Syene is 5000 stadia

7º12΄ : 5000 = 360 º : x

x = 250,000 stadia (it’s about 29,000 statute miles)

Current value is 24,907 status miles

Geographic Coordinates

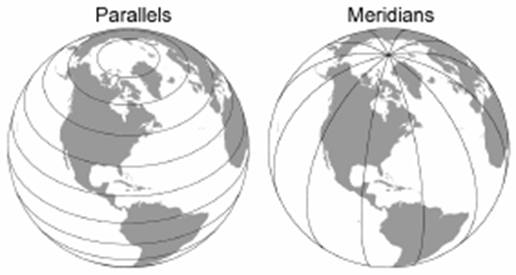
Parallel: line parallel to equator

Meridian: line perpendicular to parallel; converge at the north and south poles

Graticule: arrangement of parallels and meridians

Latitude and longtitude is the numbering system for parallels and meridians

Geographic latitude and longitude

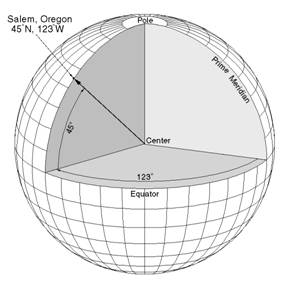
Longitude is the offset angle at the equator from prime meridian

Latitude is the angle from the equator to the place of interest

Expressed in degree, minute, and second

Can be converted into decimal degree (= degree + minute/60 + second/3600)

South latitude and west longitude is often labeled by a negative sign instead of the letters S and W in the computer

Determining time difference based on longitude

360 degree: 24 hour = ? degree: 1 hour

Every 15 degree strip becomes a time zone

Longitude for Seattle is 122º 17′ W, then what would be the time difference from London?

Longitude for Sydney, Australia is 151 º 1′ E, then what would be the time difference between Seattle and Sydney?

24pm 12pm 0am

Unfolded geographic coordinate grid (don’t forget this grid necessarily gives very much distorted image at the high latitude)

Prime meridian is located at the center

Edges are the international datelines where a day changes

Properties of the Spherical Graticule

As meridians are converging toward the pole, the length of a degree of longitude, measured east-west along parallels decreases from the equator to the pole.

The ground distance of a degree of longitude at the equator would be earth’s circumference divided by 360 (=69.2 mile)

What would be the ground distance of a degree of longitude at 50° North?

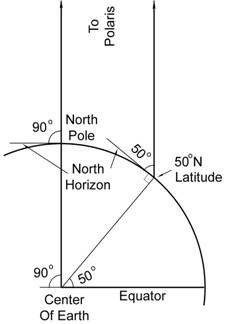
Cos 50 º = x / r

where r is the radius of the earth, x is the length of red line

x = cos 50 º * r

Circumference (2πr) is proportional to radius

So r can be replaced with the length of one degree longitude at the equator

Cos 50º * 69.2 = 0.642788 * 69.2 = 43.83811 mile

The ground distance of one degree longitude at 60 º will be the half that of one degree longitude at the equator because cosine 60 º is 0.5

Great circle

Can be obtained by cutting the earth in half (cutting the earth so that it passes through the center of the earth)

Gives the shortest route

Used in air navigation

Shortest route between Seoul and Seattle

Geodetic Coordinates

Is the earth a perfect sphere?

Not really

It’s more close to ellipsoid (more flattened at the equator)

Why is that?

Measurement of the location of geographic feature based on ellipsoid-like earth would be more accurate than based on the sphere-like earth.

More accurate measurement of coordinates based on ellipsoid is called geodetic coordinates (Why more accurate? Because ellipsoid is a better approximation of size/shape of the earth)

There are more than one reference ellipsoids used in real world. Some ellipsoid fits the best in some area. For example, a red dashed line fits the best in the upper left, but it fits the other side of the earth very poorly (see lower right).

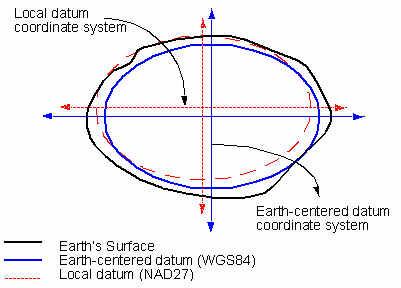
US mapping agency has used North American Datum 1927 (NAD27) until 20 years ago. It is based on reference ellipsoid called Clark 1866. Different countries have used different ellipsoid (see Table 1.2) which gives the best fit for them. Better knowledge of the earth’s shape and size and better surveying methods led to the creation of a new horizontal reference datum, the North American Datum (NAD83) in the U.S.

As GPS gets increasingly popular, it is necessary to define earth-centered datum (ellipsoid) so that coordinates are measured relative to a single (uniform) reference ellipsoid. WGS84 is earth-centered datum, and coordinate values given by GPS is measured on the basis of this datum.

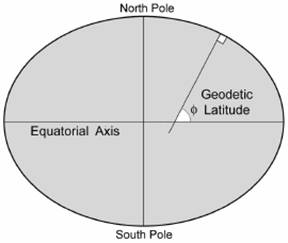
Geodetic coordinates are based on an oblate ellipsoid; geodetic latitude is the angle between the equator and the line perpendicular to the point of interest (see below)

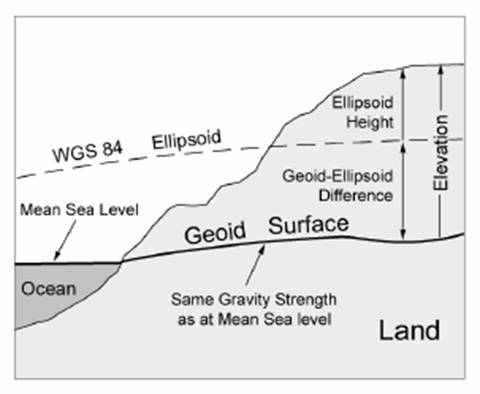
Earth as a Geoid

Elevations and water depths are measured relative to vertical reference datum

Elevations are measured relative to mean sea level (MSL)

MSL is the average of all low and high tides at a particular location over a 19 year lunar period

In principle, MSL is the surface of same strength of gravity

MSL can be extended to the land area

Such surface is not same as ellipsoid due to varying land density (thus gravity, leading to undulating surface)

This approximation of the earth that serves as the basis for vertical value measurement is called geoid

Review questions

How are longitude and latitude determined?

Is parallel a great circle?

How are geodetic coordinates different from geographic coordinates?

What is an oblate ellipsoid?

What is a geoid?

Would spot elevation (read from contour maps) be necessarily the same as z-value obtained from GPS receivers. (GPS uses WGS84 as the basis for x,y,z measurements)?